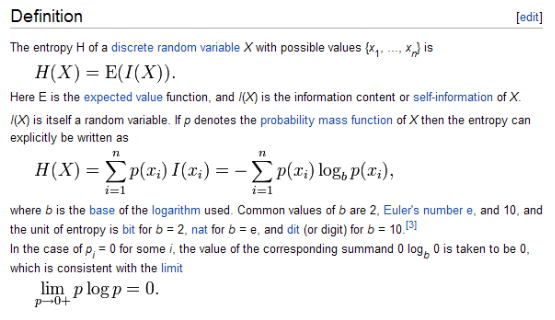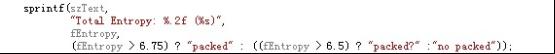第一章、你加壳了吗?
第1节、信息熵(Entropy)
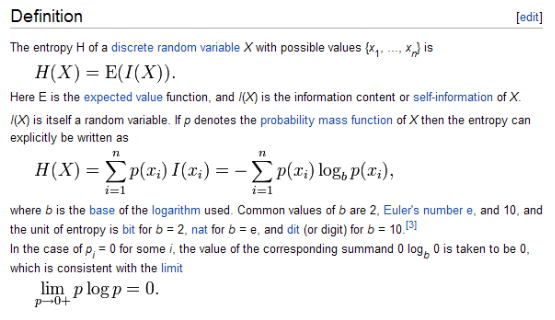
引用自:http://en.wikipedia.org/wiki/Information_entropy
一开始是否被上面这恐怖的定义吓到了?按照国内理科类教课书和论文的惯例----将公式推导和定义放在一开始,目的就是吓人。潜台词是接下来内容可信度很高很牛B。
如果你真的被吓到了,那么我的目的也就达到了。但是我的潜台词是这个理论的确很牛B,但是我们完全不需要理会它也可以。
“信息熵”是通信领域的一个概念。以我的理解就是在一段的数据中其所携带的信息量。应用在判定PE是否加壳时,“信息熵”可以这么理解,计算一个PE文件的信息量或者其中某段(Section)的信息量。当这个熵的值超过一定阈值时,则该PE或某段被加壳(Packed)。说得更准确(更通俗)些,就是压缩数据往往携带着更多的信息量,PE文件携带信息量得多的就意味着可能被加壳了。
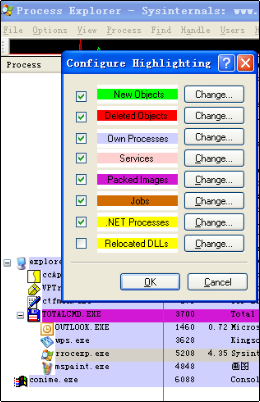
在PEiD中就有这样的功能:
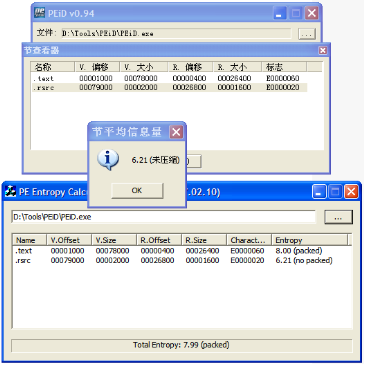
(该图片引用自小喂的帖子http://bbs.pediy.com/showthread.php?t=39443)
计算一个节或者一个PE文件的熵,可以从论坛中小喂的帖子下载到源代码。
小喂的代码的核心算法就是一个函数(一句话):
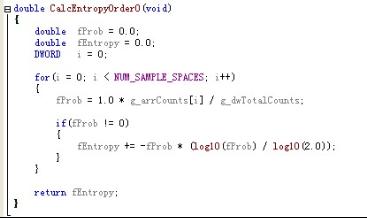
对于判定是否加壳的Entropy阈值定义如下:
加壳(Packed): Entropy > 6.75
可能加壳(Maybe Packed): 6.75 > Entropy > 6.5
无壳(No Packed): 6.5 > Entropy
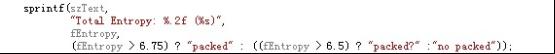
ps.关于这个定义的来源我一直没弄明白。这是order-0 entropy的定义如此,还是经验所得?
到这里基本的理论已经介绍完毕了,这章结束了吗?还没有!
当你将这套代码做测试的时候,你会发现它的误判和漏判率非常的高。当我发现这个情况的时候,我尝试使用PEiD来对比,结果让我大吃一惊。PEiD计算的Entropy和用小喂代码计算的Entropy竟然完全不一样!(貌似计算一个Section的Entropy是一样的)而且PEiD判定的命中率非常之高。
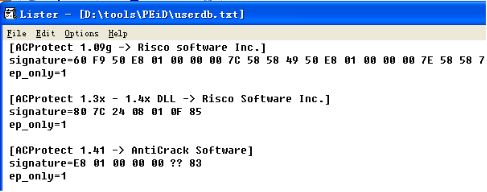
我非常想知道PEiD是如何做到的,于是通过google我来到PEiD的官方论坛。在论坛中有一个帖子引起了我的注意。
http://www.peid.info/forum/viewtopic.php?t=42
巫术(voodoo)?!啊哈,别开玩笑了。对于客户端程序来说可没有秘密可言!:D
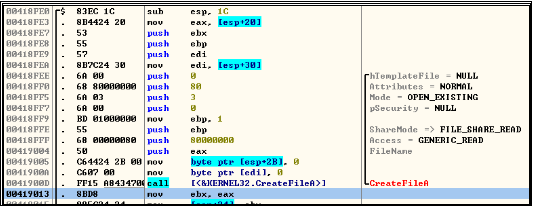
既然人家作者不愿意说,那我只好踏上PEiD的逆向分析之路。
很抱歉的是由于逆向是在07年时完成的。现在已经找不到自己当时逆向的一些注释或者资料。所以这个部分就略过吧 -- 我想你也不是很感兴趣。
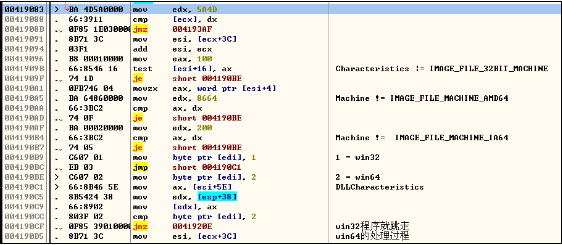
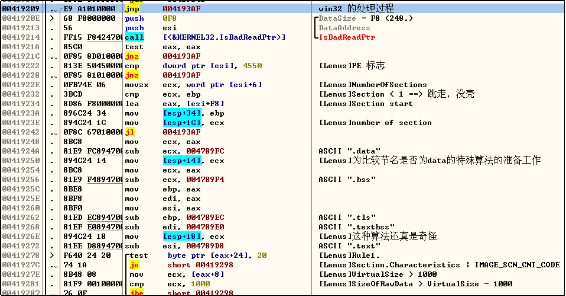
下面进入结论阶段,让我们看看PEiD都做了哪些工作。
1.重新组织需要计算的数据
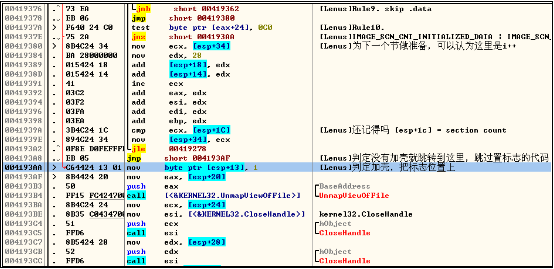
i.以下数据不列入计算熵的范围:导出表数据、导入表数据、资源数据、重定向数据。
ii. 尾部全0的数据不列入计算熵的范围。
iii. PE头不列入计算熵的范围。
2.分别计算每一部分数据的熵E和该部分数据大小S。
3.以下列公式得到整个PE文件的熵 Entropy = ∑Ei * Si / ∑Si (i = 1,2…n)。
经过上面的条件限制和方法,我计算出来的Entropy与PEiD的就基本上一样了。尝试使用100个加壳的样本和100个没有加壳的样本进行测试得到下面的数据:
1.当定义Entropy > 6.5 为 Packed时,误报率是20%左右;遗漏样本在10%以下
2.当定义Entropy > 6.75为 Packed时,误报率是10%左右;遗漏样本在15%左右
实际应用当中,针对具体的需求我还对代码和阈值做了一些微调。不过很抱歉这部分代码不能共享出来。