第六部分 SIB

    在386以前16位寻址模式下，要想操作一个多维数组或结构体数组是非常困难的，考虑下面的数组：
    
    Array2D  dword  Nrow dup (Ncol dup(?))
    
    那么我们要想存取Array2D[rowIndex][colIndex]，那么我们该怎么做呢？由于2维数组映射到内存中是一维的，那么Array2D[rowIndex][colIndex]的偏移地址就可以这么计算了：

    Effect Address = BaseAddress + (rowIndex * colSize + colIndex) * ElementSize;
    
    这里BaseAddress = Array2D，colSize = Ncol，ElementSize = sizeof(dowrd) = 4；我们看看16位寻址模式下我们该如何获取该地址：

    mov  ax, Ncol
    mul rowIndex
    add ax, colIndex
    add ax, ax    ; () * ElementSize，可用shl ax, 2代替
    add ax, ax          
    mov bx, ax          ; 16位寻址模式下能用的只有基址寄存器和索引寄存器
    
    这样dword ptr [bx]就是我们需要操作的对象了。当这个数组存储的是结构体的时候，可能还要用[bx + disp]的方式寻址到结构体内的成员。大家可以看到，简单的2维数组的操作就需要这么多指令，而当数组是3维或更大的维度的时候，这个过程的复杂程度还要增加。

    386以后，除了寻址大小变成32位，寻址模式上有了很多的改进，所有的寄存器都参与寻址，是一个方面（至少可以省掉上面的一条指令）。最重要的Intel引入的新的寻址方式基址+ 标量索引（SIB）寻址方式，这种寻址方式的引入大大简化了数组内存的存取过程。我们来看看什么是SIB寻址方式：
    
    [base + index * n + displacement]

    这跟前面的[寄存器 + displacement]的寻址的一个重要的区别是多了一个Index * n，注意，这个部分是在指令执行的过程中运算的，跟一些在汇编期间进行的乘法运算有着本质的区别（例如[ebx + 标签常量 * 2]等）。这里的base和Index为8种通用寄存器中的任意一种。n的值不能是任意的，只能是2，4，8中的一个。在往下继续解释之前，我们看看上面的算法用32位寻址模式写可以怎么写：

    mov eax, Ncol
    mul rowIndex
    add eax, colIndex

    这样dword ptr[eax * 4]就是我们要操作的对象了。当操作一维的结构体数组的时候，SIB的寻址模式将比传统的寻址模式有更大的优势。关于寻址模式和数组，结构体等的操作的例子和分析Art of assembly中的第四章和第五章有详细的介绍，给出这两章的下载：Ch04.pdf  Ch05.pdf

    6.1 SIB各个bit的涵义

    SIB的长度是固定的，只有一个字节，共8bit。我们从SIB寻址方式的定义中就可以大致推测出SIB的结构。
    
    [base + index * n + displacement]，n = 2, 4, 8，displacement是后续字节

    base和index分别为8个通用寄存器的一种，则各需要3个bit来进行编码，剩余的只有2个bit，显然用来编码n的值。2个bit也只能编码4个值，这恐怕就是为什么n只能取(1), 2, 4, 8的原因了。剩下的问题就是这些bit是如何在SIB这个字节中划分的，看看下图：

        

    跟ModR/M的划分有些相似都是2 : 3 : 3形式的。我们可以分析一下，8个base编码 * 8个Index编码 * 4个n = 256SIB寻址方式，Intel完完全全地利用SIB中的每一个bit进行编码。Intel把这256中寻址方式编码到一张表格中，看看这张表格：

    

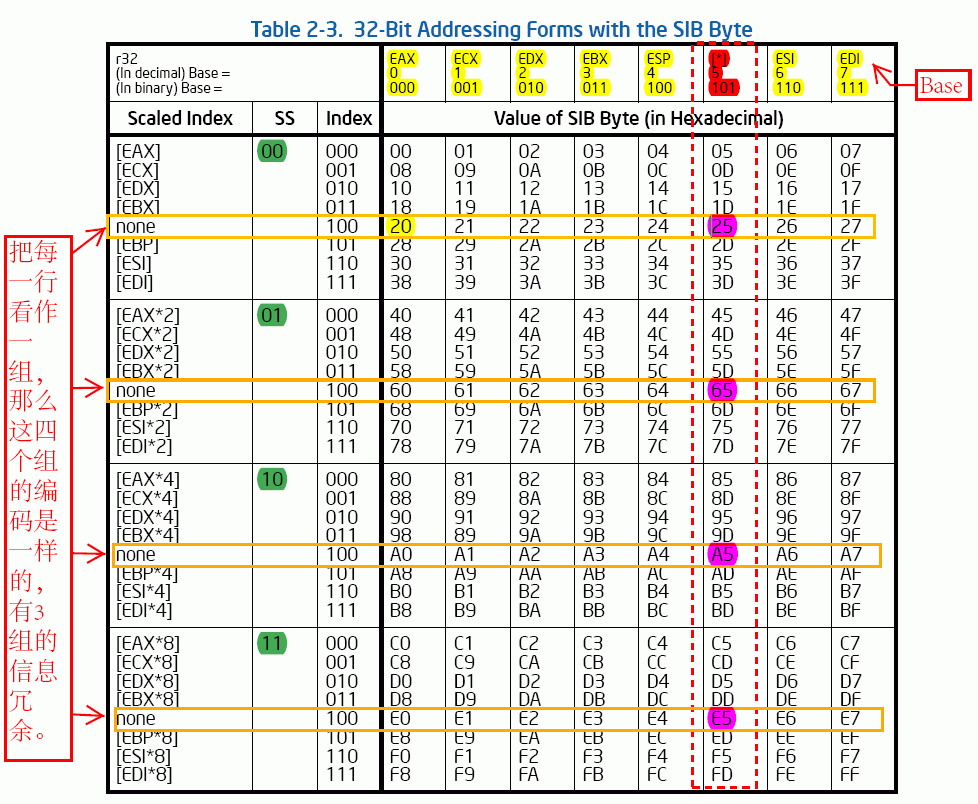
    6.1.1 Scal（SS）

    Scal在表格中用SS表示，共2bit编码了4种值1, 2, 4, 8。很明显：
    
    n = 2^SS = 1 shl SS

    在编写解析代码的时候，只需要提取出SS的值就可以知道相应的寻址模式，可以想见，SIB的解析代码要比普通的ModR/M的解析代码简单得多。

    6.1.2 Index

    这里Index编码了通用寄存器，Index和n值共同构成了Scaled Index。看看Scaled Index这一列，我们可以看到编码esp的地方被none代替了，这里的none表示什么也没有的意思，也就是这种编码方式中Scaled Index部分不存在即[base + [disp8/32]]的形式，这就跟前面的[寄存器 + disp8/32]寻址方式在形式上没有任何区别了，但实际上ModR/M+SIB的形式要多一个字节的代码。这里我们也能看到，intel取消了对esp * n的Scale Index的寻址方式，这张256种新式的表格中出现了冗余，看看下面的指令组：

    0040101B      890420                mov     dword ptr [eax], eax
    0040101E      890460                mov     dword ptr [eax], eax
    00401021      8904A0                mov     dword ptr [eax], eax
    00401024      8904E0                mov     dword ptr [eax], eax
    
    89为mov指令，04为ModR/M，Mod = 00，R/M = 100指示内存由后续的SIB字节编址。20，60，A0，E0在表格中分别对应着4个不同SS的none(100)那一行的编码中的一个。看图中橘黄色的部分，这四组的编码实际上是相同的。这些对我们的解码没有任何影响，但是我们要知道，这些冗余信息的存在。此外，SIB的256种编码模式在形式上包含了前面ModR/M的所有内存寻址方式。看看上面那条指令的短编码：

    00401028      8900                  mov     dword ptr [eax], eax
    
    事实上，ModR/M中所有的内存寻址方式都可以由多一个字节相应的SIB代替，而且替代方式不止一种。一般情况下指令肯定是越短越好，但实际应用中也可能会需要一些相同的长指令来替代，这种时候，就可以考虑这多一个字节的ModR/M + SIB编码方式了。

    6.1.3 base

    base作为基址，在编码寄存器的时候也有例外发生。看看上面表格中的红色标记（base = 101），这里的[*]本来是应该编码ebp的。这里intel是这样解释这个部分的：当Mod = 00的时候，[*]就表示空，即none什么也没有，而当Mod = 01 和 10的时候(为11的时候就是寄存器，而不是内存了)，就为[ebp]。注意说的是ModR/M字节中的Mod而不是SIB这个字节中的SS。这点很容易弄混淆。表示出来就是：

    Mod    Effectiv Address
    ------------------------
    00     [scaled index] + disp32
    01     [scaled index] + disp8 + [ebp]
    10     [scaled index] + disp32 + [ebp]

    说白了就是，这个[*]在Mod = 0的时候就表示none，其他情况正常。为什么Intel要在Mod = 0的时候搞这么一个特殊的情况呢？我们前面也说到过了，SIB中包含了ModR/M中所有的内存寻址方式，在前面说的时候有一个特例是没有考虑进去的，那就是ModR/M中的寻址特例：Mod = 00 R/M = 101时候的[displacement32]寻址，也就是只有偏移地址的寻址。我想为了把只有偏移地址的寻址方式也包含在SIB中，Intel在这个位置弄出了一个特例。这样，SIB就真正意义上完完全全包含了ModR/M中所有的寻址方式了。看实际的例子更明显：

    0040102B      890425 78563412       mov     dword ptr [12345678], eax
    00401032      890465 78563412       mov     dword ptr [12345678], eax
    00401039      8904A5 78563412       mov     dword ptr [12345678], eax
    00401040      8904E5 78563412       mov     dword ptr [12345678], eax
    00401047      8905 78563412         mov     dword ptr [12345678], eax         

    当然，表格中的冗余总是存在。

    总之SIB的表格基本上内容和格式还是比较统一的，特例的情况很少，解析起来要容易得多。
   
    6.2 ModR/M、SIB、Displacement之间的关系。

    上面主要关注的是表格内容和其中的一些特殊情况，在实际的编写代码的过程中，ModR/M、SIB、Displacement三者之间的逻辑关系其实更为重要。这部分很容易犯糊涂，至少我犯过不少糊涂，经常弄混淆一些东西。下面我把我对这部分的理解整理出来。

    1、ModR/M、SIB、Displacement是一个整体。

    虽然Intel在指令的定义上把它们进行了区分，但实际上，三者是结合在一起工作的，他们就像一个结构体的三个成员，而这个结构体的目的就是为了要编码指令的一种操作对象内存操作对象（这里我们只考虑R/M用来编码内存）。只是，这三个成员可能并不全都出现，例如SIB和Displacement部分就可以不存在。我们要注意，如果要编码内存操作对象ModR/M字节是一定要存在的，而且SIB部分和Displacement部分是不能单独存在的，SIB和Displacement的出现与否只能由ModR/M来指示。通俗一点来说，SIB和Displacement是ModR/M的附属部分。主体不存在附属部分一定不存在，而主体存在附属部分也不一定存在。

    2、ModR/M的对SIB和Displacement的控制

    ModR/M和SIB的每个bit的确切涵义已经总结过了。但是这里还是把它们之间的关系整理一下（只考虑内存寻址）：

    

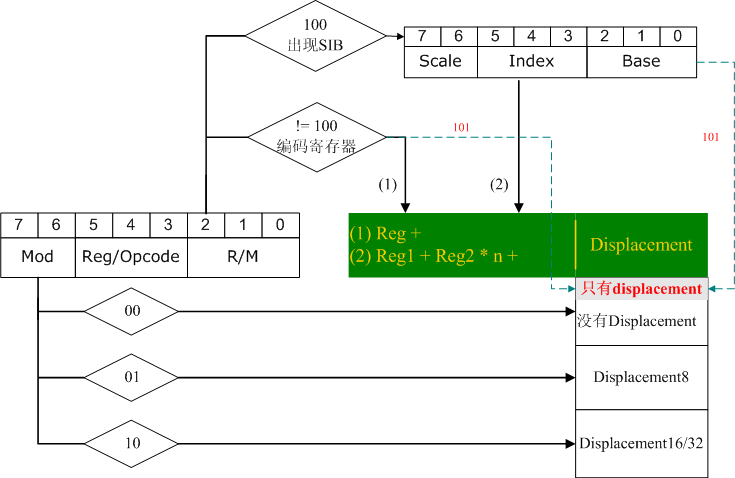
    图形绿色部分为最后解析该得到的结果。我们可以在主线中看一下得到这个结果的过程。
    
    （1）Mod决定了结果中displacement是否出现。Mod为00的时候，是没有displacement的（或者整条指令中只有一个displacement），Mod为01时dispacement为8位，通过符号扩展的方式加到前面的寄存器上，Mod为10时，偏移地址为16位/32位，取决于CPU当前工作模式。
    （2）R/M部分的编码决定了是直接编码寄存器，还是通过SIB的方式编码寄存器。
    （3）特殊情况，编码寄存器（无论是直接编码还是通过SIB的方式编码）的时候有个特殊情况，那就是，当Mod = 00并且用来编码基址寄存器的值为101(R/M = 101或者SIB.Base = 101)。整条指令中只有一个16/32位的偏移地址。

    我想上面的结构图对内存寻址方式编码的整体结构描述得很清楚了，对照这个图编写代码，出错的几率就会减少一些。

    6.3 我所知道的一些跟寻址相关的汇编小技巧。

    （1）我们看看下面的操作：

    mov ebx, eax
    add ebx, ebx
    add ebx, ecx
    add ebx, 78

    这些指令的作用很明显 ebx = eax * 2 + ecx + 78，这些指令可以用如下一条指令代替：
    
    lea ebx, [ecx + eax * 2 + 78]

    lea的执行只需要一个时钟周期，这样可以节约大概3个时钟的执行时间。在实际的逆向过程中，大家可能也会发现这种用法，这里利用的并非lea原本的意思，而是利用的SIB的编码方式能把乘法和几个加法操作合并成一条指令操作。这样的代码显然比分开add要来得快得多。

    （2）整数乘法操作

    乘法操作在intel386以前的CPU中是很浪费时钟周期的，因此有些技巧是公开而且是大家常用的。例如乘2，4，8的操作都会用shl来代替：shl x, n = x * 2^n。那么当乘数不是2的指数倍的时候该怎么处理呢？SIB可能用来替代一些简单的乘法，例如：

    imul ebx, eax, 3 => lea ebx, [eax * 2 + eax] 
    imul ebx, eax, 5 => lea ebx, [eax * 4 + eax]
    imul ebx, eax, 9 => lea ebx, [eax * 8 + eax]

    其实SIB相当于一个1248编码，10以内的数字都可以这4种形式来表示。比如
    imul ebx, eax, 7 => lea ebx, [eax * 8]
                       sub ebx, eax
    imul需要大致10左右的时钟周期，而分解后只需要大约两个时钟周期。其实任何整数N都能分解成2^n的和的形式（例如：21 = 16 + 4 + 1），这样再利用shl指令就可以把不需要乘法而完成乘法操作了，对一些不太大的整数，在对速度要求很高的场合，这样的分解是很有意义的。

    （3）CPU缓存

    这跟这里的SIB没有关系，但是跟内存的读取有些关系。CPU的设计者们发现，大多数程序在执行过程中，总会在一定的时间内存取一个范围内的内存即空间局域性。如果把当前指令存取的内存空间的预先读入一块到CPU的高速缓存区，那么指令执行速度将大大增加。当指令要读的内存不再cache中时，再到内存中去取，并刷新缓存的内容。因此，程序在设计内存的存取的时候，一般应该把要读取的数据放入连续的内存块内，这样指令hit cache的几率大大增加。有一个例子：大矩阵的乘法问题，我们知道，矩阵乘法的为行和列的交互乘法 c[i][j] = a[i][k] * b[k][j]。这里b[k][j]读取的时候违背了指令的空间局域性原则。它读取的是每rowSize的字节数的内存。因此，对于大的数组乘法，CPU需要不停地刷新cache，这样的后果就是运算速度大大降低。如果矩阵乘之前先对b进行转置操作，那么再进行乘法，读取的就是连续的区域了，这样将大大增加指令hit cache的机会。这里的是我测试用的例子cache.rar，在我的机器上（AMD64）上，差别很明显。

    Time used for algorthm1: 8.640000 seconds
    Time used for algorthm2: 2.516000 seconds
   
    感兴趣的朋友可以在自己的机器上试一下。

    汇编里还有很多这样的小技巧，其实CPU的设计者们也在不停地利用这样的一些技巧。跟内存相关的一些指令技巧，我知道的还包括对齐问题，指令流水中的等待问题，这些Art of asemmbly上都有很详细地讲解，而且有整整一章专门用来介绍汇编指令的优化问题，感兴趣的朋友可以下载下来看看(Ch03.pdf  Ch25.pdf)。
    当然，对一个程序来说，算法对性能的影响永远是第一位的。


    6.4 SIB解析代码。

    SIB和ModR/M的解析是应该联系起来的，因该说SIB的解析式ModR/M的一部分，解析ModR/M时可能会调用SIB的解析函数。
    这里还需要说明一点的时，段改写指令前缀在解析的过程中也是必须要考虑的。
    这部分的代码下载：modrm_sib_disp.rar

    运行结果：

    

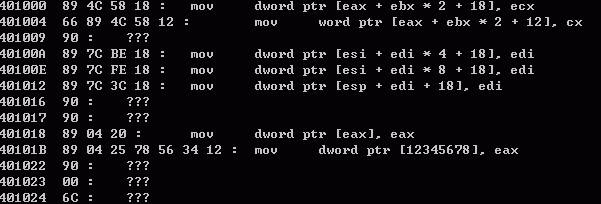
    在Od中检查一下：