DES (Weak Key,X)=X
 作者：winndy【FCG】【DFCG】【PYG】
Email：cnwinndy@hotmail.com
完稿时间：2005.12.16
如果有疑问，欢迎大家讨论。

这是密码学开卷考试的一道题目：
在DES中，若K是弱密钥，证明存在明文X，使DES（K，X）＝X。
也就是明文经DES加密后还是明文自身。

一、首先应了解什么是DES弱密钥。
  
       先从DES的解密说起：
       DES的解密过程，DES的解密过程和DES的加密过程完全类似，只不过将16圈的子密钥序列K1，K2……K16的顺序倒过来。即第一圈用第16个子密钥K16，第二圈用K15，其余类推。
       如果K16＝K1，K15＝K2，…，K9＝K8，则加密所用的子密钥与解密所用的子密钥相同，对一个明文X加密两次，得到的还是明文X。
       更强的，若K1＝K2＝…＝K16，则加密过程与解密过程完全一样。
       弱密钥的定义也就是这样定义：若k使得加密函数与解密函数一致，则称k为弱密钥。
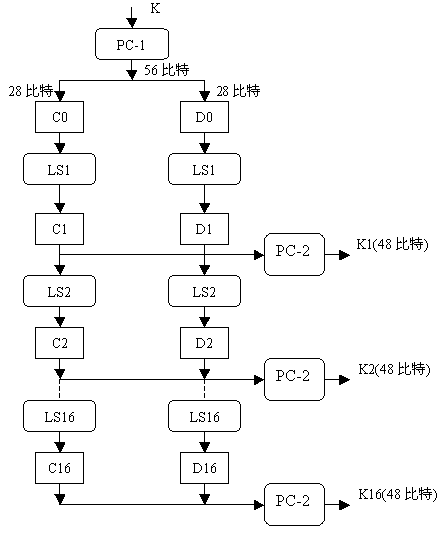
      DES至少有4个弱密钥，让我们先来看看子密钥的产生过程：
      
图片来自：风雨无阻，《公路坐标计算系统  1.0》。
http://www.pediy.com/bbshtml/BBS5/pediy50649.htm
要了解更详细的DES的流程，可参考上面的文章，这里只简要介绍一下。

 

64Bits的密钥K经PC-1之后，变为56Bits，然后分为高28Bits和低28Bits，分别进行移位。
LSi是循环左移。PC-2是从56Bits中选出48Bits输出。若C0和D0为全0或全1，则经过移位后显然不变，于是16个子密钥都相同。C0和D0是独立进行移位的，组合一下，就有4个弱密钥了。因此至少有4个弱密钥。
(1)K1＝…＝K16＝0x000000000000
(2)K1＝…＝K16＝0xFFFFFFFFFFFF
(3)K1＝…＝K16＝0x000000FFFFFF
(4)K1＝…＝K16＝0xFFFFFF000000

还可以注意到，第一组和第二组是互补的，第三组和第四组也是互补的。
事实上，对于任意密钥k，我们还有以下关系成立：（DES的互补性）
若y＝Des（k，X），则yBar＝DES（kBar，XBar）。（后缀Bar表示取补）

二、分析（逆推法）
    
刚拿到这个题目，不知怎么着手。首先想到的是从置换盒SBox着手，
                     DES的加密流程图
 

因为，如果存在明文X使得f函数的输出为0，那么由于0 Xor 0＝0，0 Xor 1＝1，那么若L0＝R0，则L1＝R2，…。最终必有R16＝L0，L16＝R0。
事实上，当我把SBox盒为0的情况都列举出来以后，根据每一种排列情况，看其是否满足E扩展后的格式，不幸的是，不存在任何X使得f函数的输出为0。

   回过头，再仔细观察DES的加密流程图，不能忽略这样一个Xor的基本性质：
      A Xor B＝C，则A＝B xor C。
同时注意到L_(i-1)=R_i，其中i＝1，…，16。
为了简化讨论，可以写出这样的序列：
L0，R0，R1，R2，…，R7，R8，…，R16。
不妨记L0＝R_-1，则有：
   
下面就利用逆向分析法，来求应满足的关系式：
 
既然L0R0加密后为R16R15，那么我们令R16＝L0，R15＝R0，然后来求R14看看。
R16＝R14 Xor f（weakkey，R15），于是R14＝R16 Xor f（weakkey，R15），
＝L0 Xor f（weakkey，R0）＝R1，继续推下去，…
R13＝R2，…，R8＝R7，…。即R_i =R_15-i ;，i＝-1，0，…7。
事实上，只要R8＝R7，就可以推出其他的等式。很容易就可以证明。
上面，得到了R8＝R7是DES（weakkey，X）＝X的必要条件。
反过来，给定R8＝R7，是否就有DES（weakkey，X）＝X成立呢？
答案是肯定的，很容易推出来。

于是，我们可以令L0＝R0，经过8圈DES加密过程，再经过IP-1，就可以得到满足要求的明文X。
我编了一个简单的程序进行了校验，结果完全是正确的。
故满足这样的要求的明文共有4×（2³²）个。
事实上，利用DES的互补性质，只需生成2×（2³²）个明文，就可以通过取反，得到另外2×（2³²）个明文。

三、小结
    思路很简单，逆推就可以了，在做注册机，分析算法后，要经常逆推，得到注册流程。虽然这么简单，但我还没发现周围的同学有独立思考出来的，甚至我给了提示，也有人想不出来。我们应该反思一下我们的教育制度了，而且是研究生教育……..